Class11th science physics(systems of particles and rotational motion)

-

What is Translational Motion?

Let us understand translational motion with the help of examples. Let’s imagine a rectangular block placed on the slanting edge of a right-angled triangle. If the block is assumed to slide down this edge without any side movement, every point in the rectangular block experiences the same displacement and more importantly, the distance between the points is also maintained.
  • In a pure translational motion, every point in the body experiences the same velocity be it at any instant of time. Both the points, P1 and P2 undergo the exact same motions. A car moving in a straight line, the path of a bullet out of a gun etc are examples of translational motion.

What is Rotational Motion?

Lets us understand this by an example. Now let us imagine a circular block going down the edge of the right-angled triangle. Examining the location and orientation of different points on the cylindrical block will tell us something new. The points on the cylindrical body experience something much different than the rectangular block. As shown by the arrows in the diagram representing the velocity, each point experiences a different magnitude of velocity in a different direction. Here the points are arranged with respect to an axis of rotation.
  • Rotation is what you achieve when you constrain a body and fix it along with a straight line. This means that the body can only turn around the line, which is defined as rotational motion. A ceiling fan, a potter’s wheel, a vehicle’s wheel are all examples of rotational motion.
  • Does the center of mass of a body necessarily lie inside the body?
    1. Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the angular momentum vector of the two particle system is the same whatever be the point about which the angular momentum is taken.
    1. Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time.
    2. We have read about the dynamics of particle motion before where we discovered that they were capable of undergoing translational motion only, but as we know, rigid bodies can undergo translational as well as rotational motion. So, in such cases, both the linear and the angular velocity need to be analyzed.
      In order to simplify these problems, we define the translational and rotationof motion of the body separately. The rotational motion of the object is referred to as the rotational motion of an object about a fixed axis. In the next section, we will discuss the dynamics of rotational motion of an object about a fixed axis.

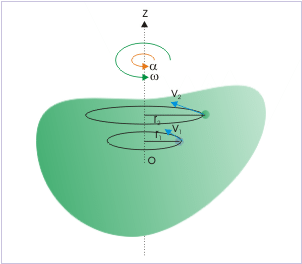
      Rigid Body Dynamics of Rotational Motion

      A rotating body, as can be seen in the figure above, will have a point that has zero velocity, about which the object undergoes rotational motion. This point can be on the body or at any point away from it. Since the axis of rotation is fixed, we consider only those components of the torques applicable on the object that is along this axis as only these components cause rotation in the body. The perpendicular component of the torque will tend to turn the axis of rotation for the object from its position.
      These results in the emergence of some necessary forces of constraint which finally tends to cancel the effect of these perpendicular components, thus restricting the motion of the axis from its fixed position, rendering its position to be maintained. Since the perpendicular components cause no effect; these components are not considered during the calculation. For any rigid body undergoing a rotational motion about a fixed axis, we need to consider only the forces that lie in planes perpendicular to the axis.
      Forces which are parallel to the axis will give torques perpendicular to the axis and need not be taken into account. Also, only the components of position vector that are perpendicular to the axis are considered. Components of position vectors along the axis result in torques perpendicular to the axis and thus are not to be taken into account.

      How to calculate net force?

      A uniform thin cylindrical disk of mass M and radius R is attached to two identical massless springs of spring constant k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane.
      The unstretched length of each spring is L.
      The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall.
      The disk rolls without slipping with velocity Vo.
      Coefficient of friction is µ.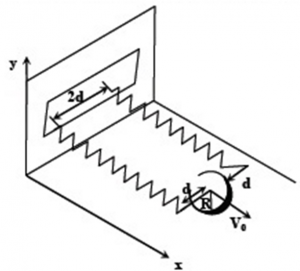
      Suppose we need to find the force when the disc is displaced by a distance ‘x’.
      It is said that the disc moves without slipping. So, the frictional force is static and hence we cannot say f = μN, instead we consider it to be ‘f’.
      Also, a = α R —– (1)
      From free body diagram, 2kx – f = ma —— (2)
      f.R = Iα  —— (3)
      Where, I = mR22 Using (1), (2) and (3)
      we get, Net force = 4kx3

Comments

Post a Comment

Popular posts from this blog

Class 11th science chemistry (thermodynamics)

-
Image
Thermodynamics deals with the change of energy in physical and chemical processes. It allows us to study these changes quantitatively as well as to make effective predictions. Therefore, we divide the universe as surrounding and system. Physical or chemical processes lead to progression or immersion of heat part of it may be converted to work. According to the first law of thermodynamics , these quantities are related as ∆U = q + w where q is heat and w is work. Change in internal energy is a state function and depends on only the initial and final states. On the other hand, w and q are not state functions. The change in temperature due to the transfer of heat one system to another system can be measured. Heat evolved or absorbed is expressed as q = C∆T. In case of expansion of gas, work is measured as w = –p ex ∆V Enthalpy Change Enthalpy change is defined as the change in energy of a system at constant pressure. It is denoted as ΔH. Enthalpy is a state function. Enthalpy ch...
Read more

Class 11th science chemistry (Redox reaction)

-
Image
Redox reaction is the combination of both oxidation and reduction reactions. When redox reaction takes place, both oxidation and reduction reactions also occur simultaneously. What is a Redox Reaction? Redox is a term used for the oxidation-reduction reaction. Redox reaction is a chemical reaction where a change in the oxidation state of atoms occurs. It involves electron transfer i.e if one chemical species gains electrons, then another chemical species gives or loses electrons. The species from which the electron is lost is said to be oxidized whereas the species to which the electron is added is said to be reduced. Example zinc displaces copper in an aqueous solution called copper sulfate. Redox reactions can be classified into four different categories: Combination reaction Decomposition reaction Displacement reaction Disproportionation reaction Oxidizing And Reducing Agents The role of an oxidizing agent (Oxidant) in a chemical reaction is to gain electrons. ...
Read more